Inhaltsverzeichnis
Am 26. Januar 2007 veranstaltete das Massachusetts Institute of Technology einen außergewöhnlichen Wettbewerb: Wer kann die größte Zahl auf eine Tafel schreiben? Während einige lauter Neunen schrieben, setzten andere auf Einsen, die weniger Platz einnehmen. Doch was wäre, wenn die Student*innen einfach weiter geschrieben hätten? Eine größte Zahl hätten sie natürlich nie gefunden.
Erst einmal könnte man meinen, unendlich sei die größte Zahl, denn keine Zahl ist größer – folglich müsste es sich um die größte Zahl handeln. Doch aus verschiedenen Gründen ist die Unendlichkeit gar keine Zahl. In einer unendlichen Menge sind alle möglichen Elemente enthalten und zwar unendlich oft. Ein Beispiel dafür sind die Nachkommastellen von Pi: Irgendwo in der Kreiszahl kommt jede mögliche Zahlenkombination vor, auch euer Geburtsdatum zum Beispiel.
Unendlich ist keine Zahl
Man spricht bei Mengen übrigens nicht von Größen oder Werten, sondern von Mächtigkeiten. Die Mächtigkeit einer Menge ist die Anzahl ihrer Elemente. Die Menge der Mitgliedsstaaten der Europäischen Union hat beispielsweise eine Mächtigkeit von 27. Die Mächtigkeit der Menge der natürlichen Zahlen ist unendlich, es gibt also unendlich viele natürliche Zahlen. Die Mächtigkeit wird mathematisch durch zwei vertikale Striche um die Menge ausgedrückt.
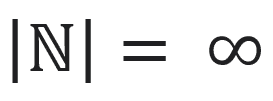
Nur weil die Mächtigkeit der Menge der natürlichen Zahlen unendlich ist, muss unendlich jedoch kein Element der Menge sein und ist es eben auch nicht, denn unendlich ist keine natürliche Zahl. Ob ein Wert selbst Element einer Menge ist, wird durch eine Art horizontalen Dreizack angegeben, ist der Wert kein Element der Menge, dann ist er durchgestrichen.

Unendlich ist also keine natürliche Zahl (dasselbe gilt auch für alle anderen Mengen – ganze, rationale, reelle Zahlen), sie hat noch nicht einmal einen definierten Wert, die Mächtigkeit der Menge der natürlichen Zahlen und die der Menge der reellen Zahlen sind zum Beispiel beide unendlich, aber dennoch nicht gleich mächtig – aber das führt zu weit. Wichtig ist, dass unendlich keine Zahl ist und deshalb kann es auch nicht die größte Zahl sein.
Auf der Suche nach der Sandzahl
Schon die alten Griechen haben sich mit riesigen Zahlen und auch mit der größte Zahl beschäftigt. So gab es etwa die Sandzahl, die Anzahl an Sandkörnern, die man bräuchte, um den Kosmos zu füllen. Sie sollte der Unendlichkeit gemäß griechischer Vorstellung sehr nah sein, doch heutzutage erscheint selbst die Sandzahl – Archimedes von Syrakus gab sie mit 1.000.000.000.000.000.000.000, also 1021, an – nur noch süß, wenn man sie mit anderen gigantischen Zahlen vergleicht.
Die Potenzschreibweise führt häufig zu Missverständnissen, einige meinen etwa intuitiv, 1020 sei das Doppelte von 1010, doch tatsächlich ist es das Zehnmilliardenfache, mit der Erhöhung der Hochzahl, des Exponenten, um eins verzehnfacht sich nämlich die Zahl. Die Anzahl der Atome im menschlichen Körper ist mit ungefähr 1027 also schon eine Millionen Mal so groß wie die ach so riesige Sandzahl.
Das Universum übertrifft all dies noch, die Anzahl der Atome im Universum ist natürlich weit höher, wie hoch genau, das vermag man nicht zu sagen, die Zahl liegt wohl irgendwo zwischen 1084 und 1089 (Nicht vergessen, das eine ist 100.000-mal größer als das andere!). Da näheren wir uns auch langsam den größten Zahlen, die in der Natur überhaupt relevant sind, die Zahl 10100, also 10.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000 wird Googol genannt, sie war in den 70ern das Rechenlimit wissenschaftlicher Taschenrechner.
Das Schachspiel beispielsweise lag lange in einem komplett unberechenbaren Bereich und noch heute ist die Anzahl möglicher unterschiedlicher Schachpartien unbekannt – die Zahl ist einfach zu groß, sie liegt irgendwo zwischen 10115 und 10120, ist also tatsächlich viel größer als die Anzahl der Atome im Universum.
Das aus China stammende Spiel Go ist noch unglaublich viel komplexer, alleine die Anzahl der möglichen legalen Stellungen auf einem großen Go-Feld ist größer als die Anzahl verschiedener möglicher Schachpartien. Die Anzahl der möglichen Go-Partien ist völlig unbekannt, sie ist so hoch, dass selbst die Hochzahl selbst wieder eine Hochzahl ist: Sie liegt zwischen einer eins mit 1048 Nullen und einer Eins mit 10170 Nullen – in der Natur spielen solche Zahlen aber keinerlei Rolle.
Eine Millinillion und eins
Aber auch in der Theorie gibt es Grenzen, unser Namenssystem für Zahlen reicht nämlich nicht unendlich weit, irgendwann ist die Vorsilbe sozusagen wieder bei einer Millionen angekommen, das ist bei 106.000 der Fall – diese Zahl hieße somit eine Millinillion. Man kann sich jedoch kaum vorstellen, wie unglaublich groß diese Zahl ist – in der Natur gibt es eigentlich keine Anwendung mehr dafür.
| Zahl | Bedeutung |
| 149.597.870.691 | Mittlerer Abstand der Erde zur Sonne in Metern |
| 435.300.000.000.000.000 | Alter des Universums in Sekunden |
| (eins zu) 710.609.175.188. 282.000 | Wahrscheinlichkeit, dass Michail Gorbatschow der Antichrist ist |
| 18.446.744.073.709.551. 615 | Anzahl der Reiskörner auf einem Schachbrett, wenn auf jedem Feld doppelt so viele Körner liegen wie auf dem Vorherigen, begonnen mit einem |
| 1.000.000.000.000.000. 000.000 | Archimedes Angabe für die Sandzahl |
| 602.214.076.000.000.000. 000.000 | Anzahl an Teilchen in einem Mol |
| 1.000.000.000.000.000. 000.000.000.000.000 | Geschätzte Anzahl der Lebewesen auf der Erde |
| 340.282.366.920.938.463. 463.374.607.431.768.211. 456 | Anzahl möglicher IP-Adressen nach dem IPv6-Protokoll |
| 100.000.000.000.000.000. 000.000.000.000.000.000. 000.000.000.000.000.000 | Ungefähre Masse des beobachtbaren Universums in Kilogramm |
| 100.000.000.000.000.000. 000.000.000.000.000.000. 000.000.000.000.000.000. 000.000.000.000.000.000. 000.000.000.000.000.000 | Obergrenze der Anzahl der Atome im beobachtbaren Universum |
| 10.000.000.000.000.000. 000.000.000.000.000.000. 000.000.000.000.000.000. 000.000.000.000.000.000. 000.000.000.000.000.000. 000.000.000.000 | Ein Googol, früheres Rechenlimit wissenschaftlicher Taschenrechner |
| 208.168.199.381.979.984. 699.478.633.344.862.770. 286.522.453.884.530.548. 425.639.456.820.927.419. 612.738.015.378.525.648. 451.698.519.643.907.259. 916.015.628.128.546.089. 888.314.427.129.715.319. 317.557.736.620.397.247. 064.840.935 | Anzahl der legalen Stellungen auf einem 19×19 Go-Spielbrett |
| 19.500.551.183.731.307. 835.329.126.754.019.748. 794.904.992.692.043.434. 567.152.132.912.323.232. 706.135.469.180.065.278. 712.755.853.360.682.328. 551.719.137.311.299.993. 600.000.000.000.000.000. 000.000.000.000.000.00 | Mögliche Kombinationen eines 7*7-Zauberwürfels |
| 1.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000.000. 000.000.000.000.000.000 | Ende unseres Namenssystems für Zahlen – eine „Millinillion“ |
Doch im Vergleich zu den wirklich großen Zahlen der Mathematik erstreckt sich unser Zahlensystem und auch seine größte Zahl nur über einen winzig kleinen Bereich. Und vollkommen irrelevant sind noch größere Zahlen auch nicht, sie kommen zwar nicht in unserem Alltagsleben vor, wenn man über die Zukunft des Universums und vielleicht sogar das Ende des Universums spricht, dann sind sie durchaus wichtig.
In sehr, sehr ferner Zukunft etwa werden alle Sterne und größeren Körper im Universum zu Eisenkugeln zerfallen sein und in noch viel fernerer Zukunft werden diese wiederum zu Schwarzen Löchern werden – die Jahreszahl für dieses Ereignis ist eine Eins mit 1026 Nullen. Eine so hohe Zahl kann man sich unmöglich vorstellen: Würdet ihr sie auf DIN A4-Blättern notieren und diese dann aufstapeln, dann würde dieser Stapel bis zum fast 1.000 Lichtjahre entfernten Stern Rigel reichen.
Doch selbst diese Schreibweise genügt nicht, um die größten Zahlen auszudrücken, mit denen Mathematiker*innen hantieren – in der Natur haben sie keinerlei Relevanz mehr, denn sie übersteigen selbst die räumlichen und zeitlichen Ausmaße unseres Universums in jeder Einheit um Längen.
Grahams Zahl und Kruskals Baum
Normalerweise bestehen Formeln und Gleichungen aus verschiedenen Zahlen, doch einige Zahlen sind so groß, dass sie selbst wiederum nur durch Formeln dargestellt werden können, so groß, dass wir gar nicht genau wissen wie groß, da die Lebensdauer des Universums für ihre Berechnung nicht genügt – diese Zahlen sind zu groß für unser Universum.
Grahams Zahl ist eine solche Zahl und häufig wird sie als größte Zahl oder größte Zahl, die in einem mathematischen Beweis verwendet wird, bezeichnet, sogar im Guiness-Buch der Rekorde. Tatsächlich sind ihre Ausmaße unvorstellbar, sie kann nur durch die sogenannte Pfeilschreibweise ausgedrückt werden. Dabei wird angegeben, wie oft eine Zahl mit sich selbst potenziert wird. Der Ausdruck 4↑↑3 bedeutet etwa, dass man die vier dreimal potenziert, also vier hoch vier hoch vier:
Vier hoch vier ergibt 256, hoch vier ergibt dann 4256, also eine Zahl mit 256 Nullen. Der harmlos aussehende Ausdruck 4↑↑3 beschreibt also schon eine Zahl, die um Größenordnungen größer ist als die Anzahl der Atome im Universum. Fügt man mehr Pfeile hinzu, werden die Zahlen schnell absurd groß. Für Grahams Zahl jedoch genügt das noch nicht, den Anfang macht hier die Rechnung 3↑↑↑↑3, schon das ergibt eine unvorstellbare große Zahl. Diese Zahl jedoch gibt lediglich die Anzahl der Pfeile für die nächste Runde an – und das ganze wiederholt man dann 64 Mal!
Natürlich kann niemand eine solche Rechnung ausführen, schließlich müsste die drei schon beim ersten Schritt über sieben Billionen Mal potenziert werden. Obwohl man den genauen Wert der Zahl also nicht kennt und wohl auch nie kennen wird, hat die Zahl jedoch eine gewisse Relevanz, sie wurde vom US-amerikanischen Mathematiker Ronald L. Graham im Rahmen eines mathematischen Problems formuliert, welches die Obergrenze möglicher Kombinationen verschiedener Objekte betrifft.
Obwohl Grahams Zahl so groß ist, dass kein Computer sie berechnen kann, ist es übrigens möglich, ihre letzten Stellen herauszufinden. Sie lauten:
02425950695064738395657479136519351798334535362521 43003540126026771622672160419810652263169355188780 38814483140652526168785095552646051071172000997092 91249544378887496062882911725063001303622934916080 25459461494578871427832350829242102091825896753560 43086993801689249889268099510169055919951195027887 17830837018340236474548882222161573228010132974509 27344594504343300901096928025352751833289884461508 94042482650181938515625357963996189939679054966380 03222348723967018485186439059104575627262464195387.
Grahams Zahl ist nicht die einzige Monsterzahl, die einmal den Titel „größte Zahl“ trug, ebenfalls sehr groß – auch wenn nicht annähernd so groß wie Grahams Zahl – ist die sogenannte Skewes-Zahl, die der Primzahlenforschung entstammt. Würde man die Skewes-Zahl auf einem quadratischen Blatt Papier notieren, hätte dieses Blatt eine Seitenlänge von einer eins mit 4,426*1033 Nullen – in Lichtjahren gemessen. Würde man Schach spielen und jedes Proton im Universum wäre eine Figur, dann entspräche die Anzahl der möglichen Züge in etwa der Skewes-Zahl.
Doch obwohl sowohl die Skewes-Zahl als auch Grahams Zahl immer wieder fälschlicherweise als größte Zahl bezeichnet werden, beide könnten genauso gut gleich eins sein, wenn man sich die aktuell größte Zahl, die in einem mathematischen Beweis verwendet wurde, ansieht. Sie steht in Verbindung zum sogenannten Baum-Theorem des US-amerikanischen Mathematikers Joseph Kruskal.
Das Spiel mit den Bäumen
Die Zahl, über die ich spreche, trägt den unscheinbaren Namen TREE(3), für eine direkte Notation als Potenz ist sie natürlich ebenfalls viel zu groß. Sie ist so groß, dass der Unterschied zwischen eins und Grahams Zahl neben ihr kaum auffällt, so groß, dass das gesamte beobachtbare Universum zu klein für sie wäre, selbst wenn man Grahams Zahl auf einen Golfball schrumpfen würde, so groß, dass euch die Atome ausgingen, wenn ihr versuchen würdet, jedes einzelne Atom im Universum zu nummerieren, lange bevor ihr auch nur in die Nähe der Zahl kämet und so groß, dass euer Gehirn zu einem Schwarzen Loch würde, lange bevor ihre jede Stelle der Zahl dort gespeichert hättet.
Kruskals Gedankengänge genau zu verstehen, ist sehr schwierig, ich würde lügen, wenn ich sagen würde, dass ich alles nachvollziehen kann. Aber zumindest in Ansätzen lässt sich TREE(3) verstehen. Es geht nämlich um Bäume und Wälder. Also natürlich nicht um die Bäume und Wälder, die in der Natur vorkommen, obwohl man sich das Baum-Theorem tatsächlich ganz gut durch diese veranschaulichen kann.
In der Mathematik ist ein Baum nichts anderes als ein verzweigter Graph, zeichnet man nun mehrere Bäume, dann spricht man von einem Wald. Kruskal dachte sich eine Art Spiel aus, man muss Samen legen (die durch verschiedenfarbige Punkte symbolisiert werden), um möglichst viele Bäume aneinander zu ketten, aber es gibt zwei Spielregeln:
1. Der erste Baum darf höchstens aus einem Samen bestehen, der zweite höchstens aus zweien, der dritte höchstens aus dreien, der vierte aus vieren und so weiter. Es ist also beispielsweise nicht zulässig, einfach aus einem Samen drei oder vier neue erwachsen zu lassen.
2. Das Spiel endet, wenn ein Baum zwangsläufig mit einem bereits vorgekommenen Baum identisch ist, dann „stirbt der Wald ab“.
Die Frage ist nun: Wie viele Bäume können gepflanzt werden, bevor dies der Fall ist? Hat man nur eine Art von Samen, dann kann logischerweise nur ein Baum gepflanzt werden, der nächste könnte sich schließlich in keinerlei Hinsicht vom ersten unterscheiden, wäre also identisch. Man schreibt also:
TREE(1) = 1
Bei zwei verschiedenen Samen sieht es schon etwas anders aus. Angenommen wir symbolisieren die unterschiedlichen Samen durch einen weißen und einen schwarzen Punkt, dann könnten wir als ersten Baum nur einen schwarzen Punkt zeichnen, als zweiten Baum könnten wir zwei weiße Punke verbinden und als dritten Baum einen einzelnen weißen Punkt nehmen. Würden wir nun zwei schwarze Punkte verbinden, denn entspräche der Endpunkt dieses Baums (ein schwarzer Punkt) unserem ersten Baum – daher ist dies unzulässig und das Spiel endet nach drei Bäumen:
TREE(2) = 3
Dies kann man nun mit immer mehr verschiedenen Samen spielen.
Die unvorstellbare Größe von TREE(3)
Das klingt jetzt alles noch nicht besonders spektakulär und es scheint rätselhaft, wie daraus eine Zahl erwachsen soll, die Grahams Zahl in den Schatten stellt und gar die größte Zahl ist, die in einem sinnvollen Kontext benutzt wird, bevor die Anzahl der Samen nicht selbst viel höher ist als Grahams Zahl. Doch tatsächlich explodiert die Anzahl möglicher Bäume bei drei Samen unmittelbar auf eine gigantische Zahl. Mit drei verschiedenen Samen kann man sein ganzes Leben lang nichts anderes machen als verschiedene Bäume zeichnen (eure Eltern sind dann bestimmt stolz auf euch), eure Kinder (die ihr nicht habt, weil ihr ja euer ganzes Leben nur Bäume zeichnen sollt) könnten damit weitermachen und würden sich TREE(3) niemals auch nur nähern.
Tatsächlich hat der YouTuber Numberphile mal ein interessantes Gedankenexperiment gemacht, denn es gibt eine kürzeste sinnvolle Zeiteinheit, unterhalb derer die womöglich in diskreten Schritten vergeht – zwischen zwei minimalen Zeiteinheiten würde dann also keine Zeit vergehen. Diese minimale Zeiteinheit, die sogenannte Planck-Zeit könnte folglich der universelle Takt des Universums, eine allgemein gültige Uhr sein und schneller als die Planck-Zeit könnte im Universum nichts passieren – es ist nämlich die Zeit, die das Licht für das Zurücklegen einer Planck-Länge, der kleinsten sinnvollen Längeneinheit braucht.
Eine Planck-Zeit ist wirklich unglaublich kurz, selbst die genauesten Atomuhren kommen aktuell nicht mal in ihre Nähe was Genauigkeit angeht – daher können wir auch noch nicht überprüfen, ob die Zeit darunter wirklich in konkreten Schritten verläuft. Eine Planck-Zeit dauert gerade einmal circa 5.391247*10-44 Sekunden. Was wäre, wenn wir so schnell zeichnen könnten, dass wir einen Baum pro Planck-Zeit schreiben?
Das Universum wäre dennoch längst tot bevor wir TREE(3) erreichen. Niemand wird also je das Spiel mit den Bäumen mit drei Samen gewinnen…
Doch das schöne an der Mathematik ist ja, dass sie unendlich ist und auch TREE(3) natürlich nicht die größte Zahl. So sind schon die ersten Blitzmerker*innen darauf gekommen, einfach mal TREE(Grahams Zahl) oder TREE(TREE(3)) zu schreiben. Und ich bin mir sicher, bald werden Mathematiker*innen eine Funktion finden, die noch viel schneller wächst als die TREE-Funktion und dann wird es eine ganz neue größte Zahl geben. Denn die Differenz zwischen der Skewes-Zahl, Grahams Zahl, TREE(3) oder überhaupt irgendeiner Zahl zu der Unendlichkeit ist immer noch eine Unendlichkeit. Oder anders ausgedrückt:
„Stell Dir eine Stahlkugel vor, die so groß ist wie die Erde. Und eine Fliege, die sich einmal in einer Million Jahren darauf niederläßt. Wenn die Stahlkugel durch die damit verbundene Reibung aufgelöst ist, dann … ja dann … hat die Ewigkeit noch nicht einmal begonnen!“
Es gibt sie somit nicht und es wird sie auch nie geben, die größte Zahl.









Claude
„Für die Benennung von Zahlen nutzt man ein Schema, welches jede erdenkliche Zahl benennt.“ – genau, man benutzt eine gewisse Anzahl Symbolen, um die grösste Zahl darzustellen.
Rayo hat diesen Fakt ausgenutzt und im Rahmen eines Wettbewerbs am MIT auf der Suche nach der grössten Zahl die Grösste Zahl folgendermassen definiert:
„Die kleinste Zahl, die größer ist als jede endliche Zahl, die durch einen Ausdruck in der Sprache der Mengenlehre mit Googol-Anzahl Symbolen oder weniger benannt ist.“
http://googology.wikia.com/wiki/Rayo%27s_number
…heisst: Um die grösste Zahl überhaupt erst definierbar zu machen, müssten wir noch ganz ganz viele weitere mathematische Symbole erfinden, damit wir auf Googol Symbole kommen, um sie dann endlich definieren zu können. :p
Sieht man dich mal am Chaos Communication Congress? Dort findest du ganz viele Gleichgesinnte, die dann z.B. einen Workshop daraus machen: https://events.ccc.de/congress/2018/wiki/index.php/Session:Wondrous_Mathematics:_Large_numbers,_very_large_numbers_and_very_very_large_numbers
Es grüsst aus der Schweiz,
Claude
Dr. Stefan Graf
Bist Du Dir sicher, lieber Jason, dass es „Gogool“ und „Gogoolplex“ heißt? Ich glaube, Du meinst „Googol“ und „Googolplex“ – oder?
VG – Stefan Graf